Testing Some examples
In a specialty shop on games and games
attributes I bought a nice round die. It is fun but
is it fair?
We can run a little test to figure that out.
To do so I have rolled the die 100 times and have
recorded the number of dots that faced up (like the
5 dots in the picture).
The results can be found in the file
rounddie.sav.
|
 |
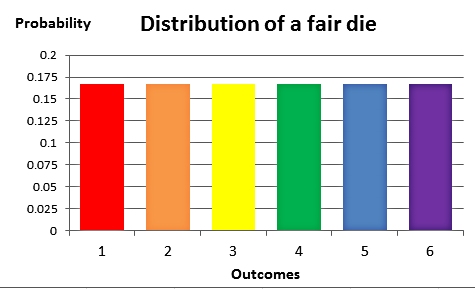
Now we all know how an ideal fair die is
supposed to roll.
There are six possible outcomes that all have the
same probability of 1/6 of facing up when the die is
rolled.
The expected average of the outcomes equals 3.5
We will run two different tests to assess whether or
not this round die is fair.
First of all we will do a one-sample t-test to find
out if the average deviates from 3.5.
And then we will run a chi-square goodness-of-fit
test to see whether the distrubution of the dots is
indeed a discrete uniform one. |
 |

Like with any test we start by specifying the hypotheses.
We write μ = the population average number of dots facing
up when rolling this round die.
H0: μ = 3.5 and
HA: μ ≠ 3.5; the test is two-tailed since we
have no indication about a direction for possible bias.
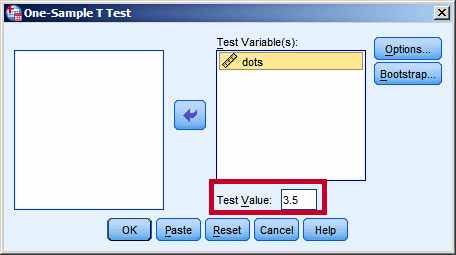
Now we run the test using SPSS; choose
Analyze > Compare
Means > One-Sample T-Test.
Note that we have to specify the Test
Value for the mean in the
appropriate field. The default setting is μ = 0, but most of
the time that is not the correct value for the mean. In our
case it is 3.5.
 |
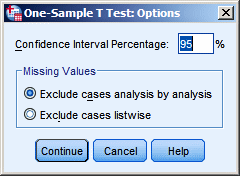
By means of the Options button we can set the
confidence interval for the mean, which is
automatically calculated by SPSS.
 |
Here is the output:
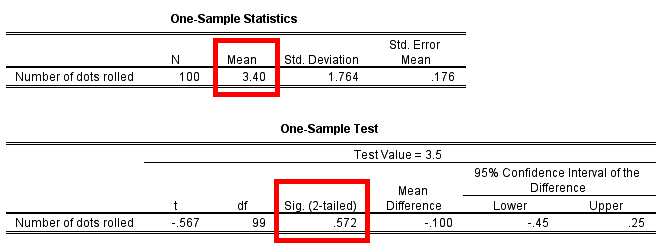
We see that the sample mean is equal to 3.4. That is not
precisely equal to the expected mean of 3.5 specified by the
null hypothesis, but the deviation doesn't seem to be large.
"Doesn't seem to be large" is quantified in the two-tailed significance
reported by SPSS. It is 0.572, which is a large significance.
Hence there is no evidence against H0. We have no indication that our die is biassed. We keep our faith in the die and in the shop that sold it.
As a useful extra we have the 95% confidence interval
that the average number of dots facing up when rolling this
die is between 3.05 and 3.75.

Again we start by specifying the hypotheses.
H0: Each number of dots has a probability of 1/6
to face up when we roll the die and
HA: Not all dots have the same probability to
face up when we roll the die.
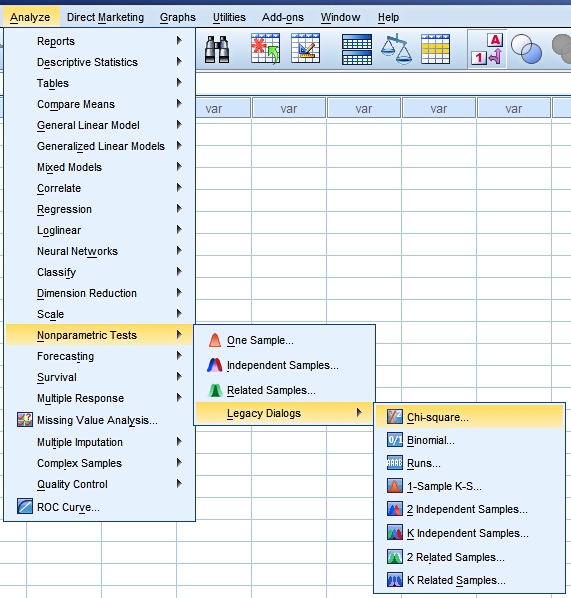
Our test can be found through Analyze
> Nonparametric tests.
In SPSS 20 there is a new approach to this group of tests.
But also the old way of asking for them is still available
through the Legacy Dialogs
 |
Note that both for the dialog boxes
and for the output there are substantial differences
between the old and the new way of performing these
tests.
In the new approach the default setting is that you
specify the type of data (One Sample, Independent
Samples or Related Samples) and the variables
involved. Based on the structure of the data SPSS
now choses the most logical test to perform. It is
named:
"Automatically choose the tests based on the data".
You can customize it if you want to.
But of course you have to make sure that the
measurement level and the role of each variable is
set properly!
In the old approach you need to know what all the
various tests in the menu are about, under which
conditions they are valid and what they do.
|
Here is the output from the new approach:

It shows little details. Only the name of the test and the resulting
significance are reported.
SPSS ends with a decision based on the default setting of a 0.05 level of
significance.
The conclusion is that there is no evidence for any bias of our round die.
Warning:
When the test is executed in this way SPSS does not check
the chi-square conditions.
When you consult the SPSS help it doesn't mention any
conditions for chi-square. However, when you check the same
chi-square test through the Legacy Dialogs the SPSS help
tells you:
Assumptions: Nonparametric tests do
not require assumptions about the shape of the underlying
distribution. The data are assumed to be a random sample.
The expected frequencies for each category should be at
least 1. No more than 20% of the categories should have
expected frequencies of less than 5.
Technical note: Consult the statistical literature and you will find that
the test statistic Σ(O-E)2/E only
asymptotically can be approximated by a chi-square
distribution. The scientists differ about when the
approximation is good enough. The strict ones demand all
expected frequencies to be larger than 5. The more lenient
ones use the assumption mentioned in the SPSS help.
Here is the output from the old approach:
 |
There is far more information about the
test results in this output.
First of all there is information about the
conditions for the chi-square test. This is shown in
footnote a. In our example there are no expected
frequencies below 5, so it is safe to use the
asymptotic significance.
We see (of cource) the same significance reported as
above. We have to draw our own conclusion.
Since the significance is 0.416 we stick to the null
hypothesis. There is no reason to doubt the fairness
of the die.
Finally in this output we see the residuals. This
gives us extra information about the differences
between the sample results and the expected counts
for a fair die.
In this case the deviations are small. The excess of
ones is not worrying. These things happen when
we have a small sample like n = 100. |

|  Helpdesk IBM SPSS Statistics 20
Helpdesk IBM SPSS Statistics 20 Helpdesk IBM SPSS Statistics 20
Helpdesk IBM SPSS Statistics 20